As we learnt in previous class that, when three line intersecting each other and make a closed figure that's called Triangle.
Tri’ means ‘three’. A triangle has three sides, three angles and three vertices. For example, in triangle ABC, denoted as D ABC
Here will learn more about the congruence of triangles, rules of congruence, some more properties of triangles and inequalities in a triangle.
A ‘congruent’ means equal in all respects or figures whose shapes and sizes are both the same.
If congruent triangles corresponding parts are equal and we write in short ‘CPCT’ for corresponding parts of congruent triangles.
If △ PQR is congruent to △ ABC, we write △ PQR ≅ △ ABC.
When △ PQR ≅ △ ABC, then sides of △ PQR fall on corresponding equal sides of △ ABC and so is the case for the angles.
SAS congruence rule : Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
ASA congruence rule : Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
The Angle-Side-Angle criterion for congruence and is written as ASA criterion.
SAS congruence rule holds but not ASS or SSA rule.
When two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal. Than we may call it as the AAS Congruence Rule.
Here we will learn some properties related to a triangle whose two sides are equal.
When a triangle in which two sides are equal is called an isosceles triangle.
Theorem 7.2 : Angles opposite to equal sides of an isosceles triangle are equal.
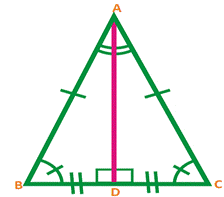
Theorem 7.3 : The sides opposite to equal angles of a triangle are equal.
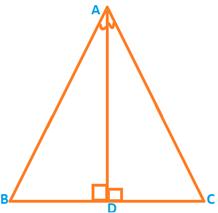
We have learnt about the equality of three angles of one triangle to three angles of the other is not sufficient for the congruence of the two triangles. But here we will learn more about the three sides of one another triangle is enough for congruence of the two triangles.
Theorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
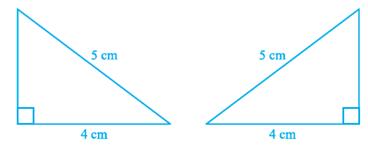
Theorem 7.5 (RHS congruence rule) : If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Note that RHS stands for Right angle – Hypotenuse – Side.
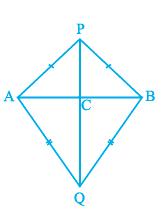
∠ PAC = ∠ PBC (Angles opposite to equal sides in DAPB)
We were learning the equality of sides and angles of a triangle or triangles. Sometimes, we learn unequal objects, we need to compare them.
Theorem 7.6 : If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater).
Theorem 7.8 : The sum of any two sides of a triangle is greater than the third side.
