We have leant that we need a minimum of two points are required to draw a line.
Here we will study about the properties of the angles formed when two lines intersect each other, and also the properties of the angles formed when a line intersects two or more parallel lines at distinct points.
A line with two end points is called a line-segment and a part of a line with one end point is called a ray.
Note that the line segment AB is denoted by AB, and its length is denoted by AB.
If three or more points lie on the same line, they are called collinear points; otherwise they are called non-collinear points.
An angle is formed when two rays originate from the same end point.
The rays making an angle are called the arms of the angle and the end point is called the vertex of the angle.
An acute angle measures between 0° and 90°, whereas a right angle is exactly equal to 90°. An angle greater than 90° but less than 180° is called an obtuse angle.
Also, recall that a straight angle is equal to 180°. An angle which is greater than 180° but less than 360° is called a reflex angle. Further, two angles whose sum is 90° are called complementary angles, and two angles whose sum is 180° are called supplementary angles.

The lengths of the common perpendiculars at different points on these parallel lines is the same. This equal length is called the distance between two parallel lines.
When the sum of two adjacent angles is 180°, then they are called a linear pair of angles.
Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.
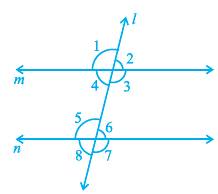
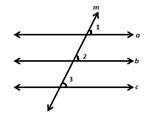
Therefore, ∠ 1 = ∠ 2 and ∠ 1 = ∠ 3
Line a || Line b
As we have learnt that the sum of all the angles of a triangle is 180°.
Theorem 6.7 : The sum of the angles of a triangle is 180°.
Theorem 6.8 : If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
