As we have learnt that a quadrilateral is a polygon with four edges and four vertices or corners.
As we learnt the joining three non–collinear points in pairs, the figure so obtained is a triangle, similarly we mark four points and see what we obtain on joining.
The sum of the angles of a quadrilateral is 360°. This can be verified by drawing a diagonal and dividing the quadrilateral into two triangles.
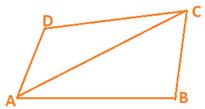
∠ DAC + ∠ ACD + ∠ D + ∠ CAB + ∠ ACB + ∠ B = 180° + 180° = 360°
Also, ∠ DAC + ∠ CAB = ∠ A and ∠ ACD + ∠ ACB = ∠ C
So, ∠ A + ∠ D + ∠ B + ∠ C = 360°.
i.e., the sum of the angles of a quadrilateral is 360°.
We had learned about the square but now we note that a square, rectangle and rhombus are all parallelograms.
A square is a rectangle and also a rhombus.
A parallelogram is a trapezium.
A kite is not a parallelogram.
A trapezium is not a parallelogram (as only one pair of opposite sides is parallel in a trapezium and we require both pairs to be parallel in a parallelogram).
A rectangle or a rhombus is not a square.
Properties of a Parallelogram
Theorem 8.1 : A diagonal of a parallelogram divides it into two congruent triangles.
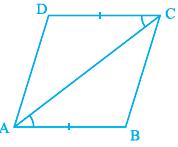
Theorem 8.2 : In a parallelogram, opposite sides are equal.
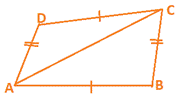
Theorem 8.3 : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
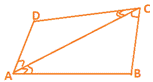
Theorem 8.4 : In a parallelogram, opposite angles are equal.
Theorem 8.5 : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Theorem 8.6 : The diagonals of a parallelogram bisect each other.
Theorem 8.7 : If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Here we will learn to verify that if in a quadrilateral any one of those properties is satisfied, then it becomes a parallelogram.
Theorem 8.8 : A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
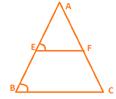
Measure EF and BC. Measure ∠ AEF and ∠ ABC.
What do you observe? You will find that :
EF = 1/2BC and ∠ AEF = ∠ ABC
So, EF || BC
Theorem 8.9 : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Theorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
