We are very familiar with the concept of the Triangles and congruent figures. Congruent means when two figures are called congruent, if they have the same shape and the same size.
The part of the plane enclosed by a simple closed figure is called a planar region corresponding to that figure. The magnitude or measure of this planar region is called its area.
We all are aware of some of formulae's to find the areas of different figures such as rectangle, square, parallelogram, triangle etc.,
In the given Figure trapezium ABCD and parallelogram EFCD have a common side DC. We say that trapezium ABCD and parallelogram EFCD are on the same base DC.
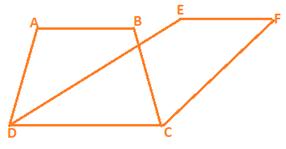
So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
Here we will learn how to find a relation, if any areas between two parallelograms on the same base and between the same parallels.
Any parallelograms on the same base and between the same parallels are equal in area.
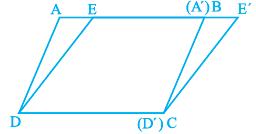
ar (ABCD) = ar (ADE) + ar (EBCD)
= ar (A'D'E') + ar (EBCD)
= ar (EE'CD)
Theorem 9.1 : Parallelograms on the same base and between the same parallels are equal in area.

ar (ABC) = ar (PBC)
Theorem 9.2 : Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
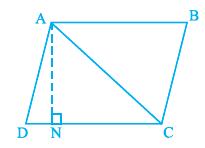
Area of D ADC =1/2 x base DC x corresponding altitude AN
Theorem 9.3 : Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
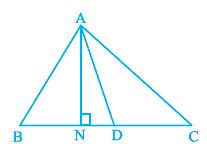
ar(ABD) = ar(ACD)
