Circle which has round in shape, such as wheels of a vehicle, bangles, dials of many clocks, coins of denominations.
In simple way we can say that anything abound us having the round in shape is called Circle. Circles have radius and diameter and one center.
The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle. The circle and its interior make up the circular region.
When any line segment joining the centre and any point on the circle is also called a radius of the circle.
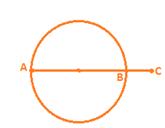
Diameter is the longest chord and all diameters have the same length, which is equal to two times the radius, both arcs are equal and each is called a semicircle.
The length of the complete circle is called its circumference. The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle.
When two arcs are equal, that is, each is a semicircle, then both segments and both sectors become the same and each is known as a semicircular region.
∠PRQ is called the angle subtended by the line segment PQ at the point R.
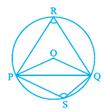
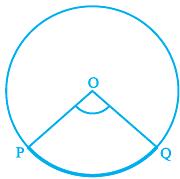
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre.
Theorem 10.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
Theorem 10.3 : The perpendicular from the centre of a circle to a chord bisects the chord.
Theorem 10.4 : The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Theorem 10.5 : There is one and only one circle passing through three given
non-collinear points.
Equal Chords and Their Distances from the Centre
In previously we have learnt that two points are sufficient to determine a line. But while we think about the circle that how many points are sufficient to determine a circle.
If the points lie on a line, then the third point will lie inside or outside the circle passing through two points.
Theorem 10.6 : Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Theorem 10.7 : Chords equidistant from the centre of a circle are equal in length.
A circle can have infinitely many chords.
The length of the perpendicular from a point to a line is the distance of the line from the point.
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
Congruent arcs (or equal arcs) of a circle subtend equal angles at the centre.
Therefore, the angle subtended by a chord of a circle at its centre is equal to the angle subtended by the corresponding (minor) arc at the centre. The following theorem gives the relationship between the angles subtended by an arc at the centre and at a point on the circle.
The end points of a chord other than diameter of a circle cuts it into two arcs — one major and other minor.
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
Congruent arcs (or equal arcs) of a circle subtend equal angles at the centre.
Theorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Theorem 10.9 : Angles in the same segment of a circle are equal.
Theorem 10.10 : If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle
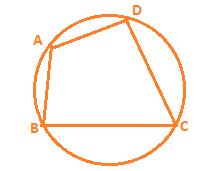
You find that ∠A + ∠C = 180° and ∠B + ∠D = 180°, neglecting the error in measurements.
Theorem 10.11 : The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.In fact, the converse of this theorem, which is stated below is also true.
Theorem 10.12 : If the sum of a pair of opposite angles of a quadrilateral is 180°, the quadrilateral is cyclic.
