We have learnt that a polynomials in one variable and their degrees. Recall that if p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial p(x). For example, 4x + 2 is a polynomial in the variable x of degree 1, 2y2 − 3y + 4 is a polynomial in the variable y of degree 2.
A polynomial of degree 1 is called a linear polynomial. For example, 2x − 3,
Polynomials such as 2x + 5 − x2, x3 + 1, etc., are not linear polynomials.
A polynomial of degree 2 is called a quadratic polynomial. The name ‘quadratic’ has been derived from the word ‘quadrate’, which means 'square’. y2 −2, 2- x2.
A polynomial of degree 3 is called a cubic polynomial. Some examples- 3 − x2 + x3, 3x3 −2x2 + x −1.
The highest power of x in p(x) is called the degree of the polynomial p(x).
A polynomial of degree 3 is called a cubic polynomial
If p(x) is a polynomial in x, and if k is any real number, then the value obtained by replacing x by k in p(x), is called the value of p(x) at x = k, and is denoted by p(k).
What is the value of p(x) = x2 −3x − 4 at x = −1? We have :
p(−1) = (−1)2 −{3 x (−1)} − 4 = 0
Also, note that p(4) = 42 −(3 x 4) − 4 = 0.
As p(−1) = 0 and p(4) = 0, −1 and 4 are called the zeroes of the quadratic polynomial x2 −3x −4. More generally, a real number k is said to be a zero of a polynomial p(x), if p(k) = 0.
The zero of the linear polynomial ax + b is −b/a = (Constant term)/Coefficient of x.
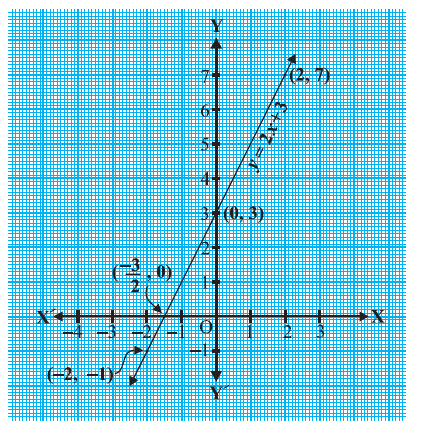
We know that a real number k is a zero of the polynomial p(x) if p(k) = 0. here we will see the geometrical representations of linear and quadratic polynomials and the geometrical meaning of their zeroes.
|
X |
-2 |
2 |
|
Y = 2x + 3 |
-1 |
7 |
y = 2x + 3
= 2 x(-2) + 3
= -4 + 3
= -1
The fact is true for any quadratic polynomial, i.e., the zeroes of a quadratic polynomial ax2 + bx + c, a ≠ 0, are precisely the x-coordinates of the points where the parabola representing y = ax2 + bx + c intersects the x-axis.
We have already seen that zero of a linear polynomial ax + b is −b/a.
a,b are Greek letters pronounced as ‘alpha’ and ‘beta’ respectively. We will use later one more letter ‘g’ pronounced as ‘gamma’.
Sum of zeroes = a + b = -b/1 = (Coefficient of)/Coefficient of b x
Product of zeroes = ab = c/a = Constant term/Coefficient of x2
We know that a cubic polynomial has at most three zeroes.
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) x q(x) + r(x),
Where r(x) = 0 or degree of r(x) < degree of g(x).
The result is known as the Division Algorithm for polynomials.
