Linear equations in two variables are equations which can be expressed as ax + by + c = 0, where a, b and c are real numbers and both a, and b are not zero. The solution of such equations is a pair of values for x and y which makes both sides of the equation equal.
Examples of linear equations in two variables:
2x + 3y = 5
x − 2y − 3 = 0
and x − 0y = 2, i.e., x = 2
An equation which can be put in the form ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables x and y.
Every solution of the equation is a point on the line representing it. each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa.
Two linear equations are in the same two variables x and y. Equations like these are called a pair of linear equations in two variables.
We have learnt that how we can graphically represent a pair of linear equations as two lines.
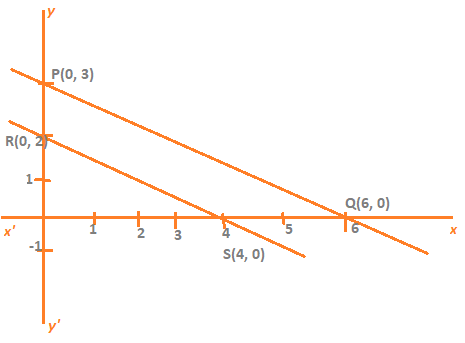
Since (4, 2) is the only common point on both the lines, there is one and only one solution for this pair of linear equations in two variables.
A pair of linear equations which are equivalent has infinitely many distinct common solutions. Such a pair is called a dependent pair of linear equations in two variables. Note that a dependent pair of linear equations is always consistent.
We have learnt how to solve a pair of linear equations graphically. The graphical method is not convenient in cases when the point representing the solution of the linear equations has non-integral coordinates like ( √3, 2√7), (−1.75, 3.3) etc.
There are several algebraic methods we will learn here.
3.4.1 Substitution Method
The substituted the value of one variable by expressing it in terms of the other variable to solve the pair of linear equations. That is why the method is known as the substitution method.
3.4.2 Elimination Method
The eliminating (i.e., removing) one variable.
To get a linear equation in one variable. In the example above, we eliminated y. We could also have eliminated x.
Cross - Multiplication Method
We have learnt more method to solve the different type of equations. Now we learn one more algebraic method to solve a pair of linear equations which for many reasons is a very useful method of solving these equations.
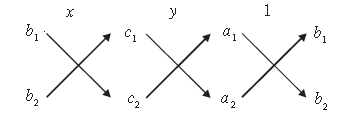
If we find the Equations −
x/b1c2 - b2c1 = y/c1a1 - c2a1 1/a1b2 - a2b1 the solution given by Equations
We will learn the solution of such pairs of equations which are not linear but can be reduced to linear form by making some suitable substitutions.
These equations are not in the form ax + by + c = 0. However, if we substitute 1/x − p and 1/y =q.
