A quadrilateral is a polygon with 4 sides, edges and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle. The total of its interior angles of quadrilaterals has 360 degrees.
A simple closed curve made up of only line segments is called a polygon.
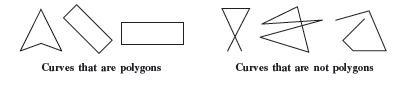
There are various types of polygons, in that you have already learnt and some of new polygons here you will learn here.
Classification of polygons
| Nubmer of Sides or Vertices | Classification | Sample Figure |
|---|---|---|
| 3 | Traingle |  |
| 4 | Quadrilateral |  |
| 5 | Pentagon |  |
| 6 | Hexagon | 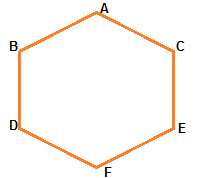 |
| 7 | Heptagon | 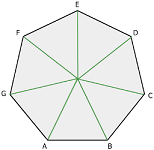 |
| 8 | Octagon | 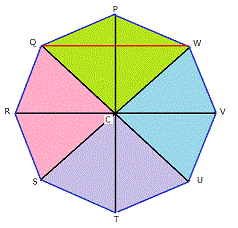 |
| 9 | Nanagon | 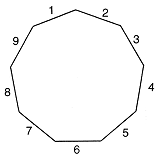 |
| 10 | Decagon | 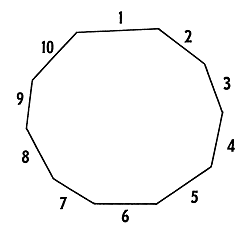 |
| ⋮ | ⋮ | ⋮ |
| n | n-gon |
A diagonal is a line segment connecting two non-consecutive vertices of a polygon
Polygons that are convex have no portions of their diagonals in their exteriors or any line segment joining any two different points, in the interior of the polygon, lies wholly in the interior of it .
A regular polygon is both ‘equiangular’ and ‘equilateral’.
A square has sides of equal length and angles of equal measure. Hence it is a regular polygon. A rectangle is equiangular but not equilateral.
The sum of the measures of the three angles of a triangle is 180°.
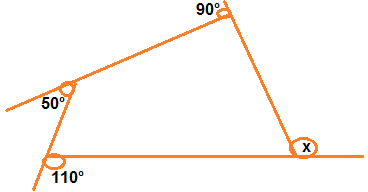
The sum of the measures of the external angles of any polygon is 360°.
On many occasions a knowledge of exterior angles may throw light on the nature of interior angles and sides.
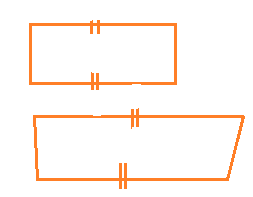
Based on the nature of the sides or angles of a quadrilateral, it gets special names.
Trapezium
Trapezium is a quadrilateral with a pair of parallel sides.
There are four sides and four angles in a parallelogram. Some of these are equal.
There has opposite sides, adjacent sides with opposite angels, adjacent angles. The opposite sides of a parallelogram are of equal length.
The opposite angles of a parallelogram are of equal measure.
The adjacent angles in a parallelogram are supplementary.
The diagonals of a parallelogram bisect each other (at the point of their intersection, of course!)
The opposite sides of a rhombus have the same length, it is also a parallelogram.
So, a rhombus has all the properties of a parallelogram and also that of a kite.
The diagonals of a rectangle are of equal length. In a rectangle the diagonals, besides being equal in length bisect each other
The diagonals of a square are perpendicular bisectors of each other.
Rhombus
A Rhombus (which, you will see, is a parallelogram) as a special case of kite (which is not a a parallelogram).
Note that the sides of rhombus are all of same length; this is not the case with the kite. A rhombus is a quadrilateral with sides of equal length.
Since the opposite sides of a rhombus have the same length, it is also a parallelogram. So, a rhombus has all the properties of a parallelogram and also that of a kite.
A rectangle
A rectangle is a parallelogram with equal angles.
A rectangle is a parallelogram in which every angle is a right angle. In a parallelogram, the diagonals can be of different lengths. (Check this); but surprisingly the rectangle (being a special case) has diagonals of equal length.
Property: The diagonals of a rectangle are of equal length.
A square
A square is a rectangle with equal sides.
This means a square has all the properties of a rectangle with an additional requirement that all the sides have equal length.
