There are many numbers used for many purpose were called counting numbers or natural numbers. we learnt the whole numbers, i.e., 0, 1, 2, 3, ... The negatives of natural numbers were then put together with whole numbers to make up integers. Integers are ..., −3, −2, −1, 0, 1, 2, 3, .....
The word ‘rational’ arises from the term ‘ratio’. Extending the number system, from natural numbers to whole numbers and from whole numbers to integers the number can be expressed as fraction include all the integers, fractions and decimal known as Rational Numbers.
The ratio of two integers p and q (≠), i.e., p:q can be written in the form p/q. This is the form in which rational numbers are expressed.
A rational number is defined as a number that can be expressed in the form p/q, where p and q are integers and q ≠ 0.
A rational number can be expressed in the form p/q. rational numbers include integers and fractions.
When multiplying the numerator and denominator of a rational number by the same non zero integer, we obtain another rational number equivalent to the given rational number.
When in any fractions of numerator and denominator of this number are positive integers. Such a rational number is called a positive rational number.
Whereas the denominator is a positive integer, Such a rational number is called a negative rational number.
We know very well how to represent integers on a number line.

The points to the right of 0 are denoted by + sign and are positive integers. The points to the left of 0 are denoted by − sign and are negative integers.
Here go to learn how the rational numbers can be represented on a number line.
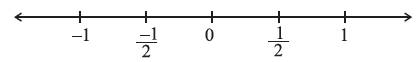
In p/q , the integer p is the numerator, and the integer q (≠ 0) is the denominator.
Mention five rational numbers each of whose
Numerator is a negative integer and denominator is a positive integer.
Numerator is a positive integer and denominator is a negative integer.
Numerator and denominator both are negative integers.
Numerator and denominator both are positive integers.
Thus, rational numbers include integers and fractions.
Here we learn a standard form of Rational Number. A rational number is said to be in the standard form if its denominator is a positive integer and the numerator and denominator have no common factor other than 1.
If a rational number is not in the standard form, then it can be reduced to the standard form.
If a rational number is not in the standard form, then it can be reduced to the standard form.
Here we learn about the comparisons of two integers or two fractions.
To compare two negative rational numbers, we compare them ignoring their negative signs and then reverse the order.

A negative rational number is to the left of zero whereas a positive rational number is to the right of zero on a number line.
As we can count the number between 3-7 are 4, 5 and 6. In similarly we can find the Numbers between Rational Numbers.
We can find unlimited number of rational numbers between any two rational numbers.
Find three rational numbers between − 2 and − 1.
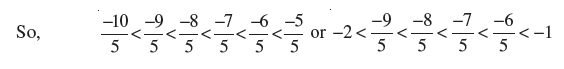
As we know how to add, subtract, multiply and divide integers as well as fractions.
Now here go to learn about these with Rational Numbers.
Addition
Find 7/3 + (-5/3)

The distance between two consecutive points is 1/3. So adding -5/3 to 7/3 will mean, moving to the left of 7/3, making 5 jumps, and We'll reach at2/3.
So,
7/3 + (-5)/3 = 7 + (-5)/3 = 2/3
While adding rational numbers with same denominators, we should add the numerators keeping the denominators same.
When we have different denominators than we should first find the LCM of the two denominators. Then, we find the equivalent rational numbers of the given rational numbers with this LCM as the denominator. Then, add the two rational numbers.
Subtraction
When we subtracting two rational numbers, we add the additive inverse of the rational number that is being subtracted, to the other rational number.
Multiplication
While we multiplying a rational number by a positive integer, we multiply the numerator by that integer, keeping the denominator unchanged.
Let us multiply the rational number -3/5 by 2, i.e., we find -3/5 x 2.

So, here
-3/5 x 2 = -3 x 2/5 = -6/5
Division
While divide one rational number by the other non-zero rational number, we multiply the rational number by the reciprocal of the other.
