A counting number, zero, or the negative of a counting number. No fractions or decimals.
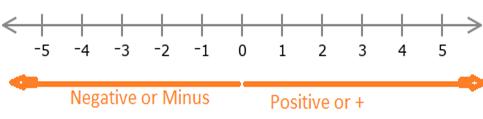
When you see on Number line before Zero (0) and after 0, use a sign going for numbers less than zero and greater that zero.
The sign that use is the placement of a minus sign before the zero numbers.
This indicates that numbers with a negative sign are less than zero. These are called negative numbers.
Tag me with a sign
We have seen yet some numbers carry a minus sign that's before zero or left hand side and some of are positive that's after zero or right hand side.
So now this is easy to find and tag the number is in minus or positive. In same way you can find about the profit and the losses. If you got in positive means you get profit and if you got the minus or negative means you get loss and many more.
A counting number that could be zero or negative or positive of a counting number. The numbers to be discovered were natural numbers i.e. 1, 2, 3, 4,... If we include zero to the collection of natural numbers, we get a new collection of numbers known as whole numbers i.e. 0, 1, 2, 3, 4,... the whole numbers and the negative numbers together, the new collection of numbers will look like 0, 1, 2, 3, 4, 5,…,−1,−2,−3,−4,−5, … and this collection of numbers is known as Integers.
You add when you have two positive integers like (+3) + (+2) = +5 [= 3 + 2]. You also add when you have two negative integers, but the answer will take a minus (−) sign like (−2) + (−1) =−(2+1) = −3.
When you have one positive and one negative integer, you must subtract, but answer will take the sign of the bigger integer (Ignoring the signs of the numbers decide which is bigger).
It is not always easy to add integers using coloured buttons. Shall we use number line for additions?

Subtraction of Integers with the help of a Number Line
We have added positive integers on a number line. For example, consider 6+2. We start from 6 and go 2 steps to the right side. We reach at 8.
So, 6 + 2 = 8.

