We have been dealing with figures that can be easily drawn on our notebooks or blackboards. These are called plane figures.
We have also understood what rectangles, squares and circles are, what we mean by their perimeters and areas, and how we can find them.
We shall now learn here to find the surface areas and volumes of cuboids and cylinders and so many.
We have learnt about the cube and cuboids that's shapes and figures. Here we will learn to find the area measurements of that.
Surface Area of a Cuboid = 2(lb + bh + hl)
Where l, b and h are respectively the three edges of the cuboids’.
Surface Area of a Cube = 6a2
where a is the edge of the cube.
When we find six faces of a cuboid, we only find the area of the four faces, leaving the bottom and top faces. In such a case, the area of these four faces is called the lateral surface area of the cuboid. So, lateral surface area of a cuboid of length l, breadth b and height h is equal to 2lh + 2bh or 2(l + b)h. Similarly, lateral surface area of a cube of side a is equal to 4a2.
So, curved surface area of the cylinder
= area of the rectangular sheet = length x breadth
= perimeter of the base of the cylinder x h
= 2Πr x h
Therefore, Curved Surface Area of a Cylinder = 2Πrh
If the top and the bottom of the cylinder are also to be covered, then we need two circles (infact, circular regions) to do that, each of radius r, and thus having an area of pr2 each, giving us the total surface area as 2Πrh + 2Πr2 = 2Πr(r + h).
Total Surface Area of a Cylinder = 2Πr(r + h)
There is another kind of solid which is not a prism (These kinds of solids are called pyramids.).
There is a right circular cone, the point A is called the vertex, AB is called the height, BC is called the radius and AC is called the slant height of the cone. Here B will be the centre of circular base of the cone. The height, radius and slant height of the cone are usually denoted by h, r and l respectively.
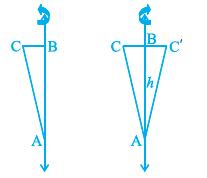
Curved Surface Area of a Cone =1/2 x l x 2pr
= Πrl
Total Surface Area of a Cone = Πrl + Πr2 = Πr(l + r)
Surface Area of a Sphere
Sphere is almost likely to a circle, because a circle is a plane closed figure whose every point lies at a constant distance (called radius) from a fixed point, which is called the centre of the circle.
Similarly with circle, sphere is a three dimensional figure (solid figure), which is made up of all points in the space, which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.
Surface Area of a Sphere = 4 p r2
The curved surface area of a hemisphere is half the surface area of the sphere, which is
1/2of 4Πr2.
Curved Surface Area of a Hemisphere = 2Πr2
Total Surface Area of a Hemisphere = 3Πr2
When any object is solid, then the space occupied by such an object is measured, and is termed the Volume of the object
When the object is hollow, then interior is empty and can be filled with air, or some liquid that will take the shape of its container. The volume of the substance that can fill the interior is called the capacity of the container.
Volume of a Cuboid = base area x height = length x breadth x height
Where l x b x h, where l, b and h are respectively the length, breadth and height of the cuboid.
Volume of a Cube = edge x edge x edge = a3
As a cuboid is built up with like rectangles of the same size, we have also seen that a right circular cylinder can be built up using circles of the same size. So, using the same argument as for a cuboid, here we will see that the volume of a cylinder can be obtained as :
base area x height
= area of circular base x height
= Πr2h
So, Volume of a Cylinder = Πr2h
where r is the base radius and h is the height of the cylinder.
Here we will find and show that the three times the volume of a cone, makes up the volume of a cylinder, which has the same base radius and the same height as the cone, which means that the volume of the cone is one-third the volume of the cylinder.
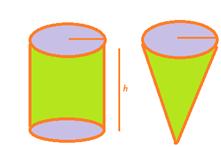
Volume of a Cone =1/3 Πr2h
We have learnt that how to find the many shapes of volumes, here will go to learn measuring the volume of a sphere.
Volume of a Sphere = 4/3Πr3
where r is the radius of the sphere.
As we know that a hemisphere is half of a sphere
Volume of a Hemisphere = 2/3Πr3
you have studied the following points:
1. Surface area of a cuboid = 2 (lb + bh + hl)
2. Surface area of a cube = 6a2
3. Curved surface area of a cylinder = 2Πrh
4. Total surface area of a cylinder = 2Πr(r + h)
5. Curved surface area of a cone = Πrl
6. Total surface area of a right circular cone = Πrl + Πr2, i.e., Πr (l + r)
7. Surface area of a sphere of radius r = 4 Π r2
8. Curved surface area of a hemisphere = 2Πr2
9. Total surface area of a hemisphere = 3Πr2
10. Volume of a cuboid = l x b x h
11. Volume of a cube = a3
12. Volume of a cylinder = Πr2h
13. Volume of a cone =1/3 Πr2h
14. Volume of a sphere of radius r =4/3Πr3
15. Volume of a hemisphere =2/3 Πr3
[Here, letters l, b, h, a, r, etc. have been used in their usual meaning, depending on the context.]
