We have learnt that a circle is a collection of all points in a plane which are at a constant distance (radius) from a fixed point (centre). Also studied various terms related to a circle like chord, segment, sector, arc etc.
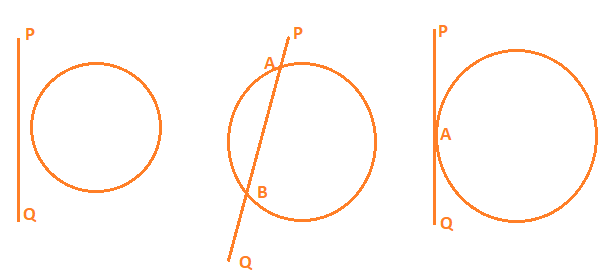
In the figure the line PQ and the circle have no common point. In this case, PQ is called a non-intersecting line with respect to the circle.
In the previous topic, we have learn that a tangent* to a circle is a line that intersects the circle at only one point.
The tangent to a circle is a special case of the secant, when the two end points of its corresponding chord coincide.
*The word ‘tangent’ comes from the Latin word ‘tangere’, which means to touch and was introduced by the Danish mathematician Thomas Fineke in 1583.
The common point of the tangent and the circle is called the point of contact and the tangent is said to touch the circle at the common point.
Theorem 10.1 : The tangent at any point of a circle is perpendicular to the radius through the point of contact.
The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent from the point P to the circle.
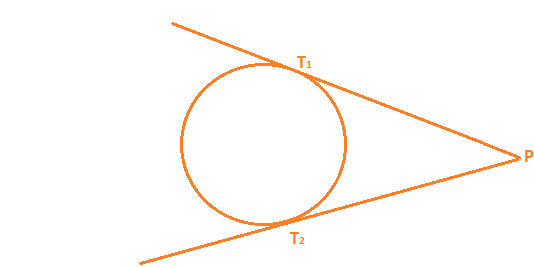
In the figure PT1 and PT2 are the lengths of the tangents from P to the circle. The lengths PT1 and PT2 have a common property.
Theorem 10.2 : The lengths of tangents drawn from an external point to a circle are equal.
