We all are more familiar with some of methods to finding perimeters and areas of simple plane figures such as rectangles, squares, parallelograms, triangles and circles.
We will learn here with a review of the concepts of perimeter (circumference) and area of a circle and apply this knowledge in finding the areas of two special ‘parts’ of a circular region (or briefly of a circle) known as sector and segment. We will also learn how to find the areas of some combinations of plane figures involving circles or their parts.
As we leant that the distance covered by travelling once around a circle is its perimeter, usually called its circumference.
We know that the circumference of a circle bears a constant ratio with its diameter. This constant ratio is denoted by the Greek letter p (read as ‘pi’).
Circumference/Diameter = Π
or, circumference = Π x diameter
= Π x 2r (where r is the radius of the circle)
= 2Πr
The great Indian mathematician Aryabhata (C.E. 476 — 550) gave an approximate value of Π. He stated that Π = 62832/20000, which is nearly equal to 3.1416.
However, for practical purposes, we generally take the value of Π as 22/7 or 3.14, approximately.
The portion (or part) of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle and the portion (or part) of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.
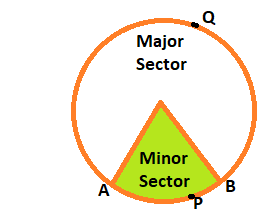
In the Figure OAPB is called the minor sector and OAQB is called the major sector. You can also see that angle of the major sector is 360° — ∠ AOB.
Area of the sector of angle q = q/360 x pr, where r is the radius of the circle and q the angle of the sector in degrees.
Here we will try to calculate the areas of some combinations of plane figures.
