A Number can be expressed as fraction that includes integers. We have learnt more about the Natural numbers that started with 1, whole numbers that started with 0 and so on.
We have seen the equations and also negative and positive integers and have much operations with those.
Here we go to learn more about the properties of the Rational Numbers.
When a number which can be written in the form p/q, where p and q are integers and q ≠ 0 is called a rational number.
A rational numbers are closed under addition. That is, for any two rational numbers a and b, a + b is also a rational number.
When rational numbers are closed under subtraction. That is, for any two rational numbers a and b, a − b is also a rational number.
When rational numbers are closed under multiplication. That is, for any two rational numbers a and b, a x b is also a rational number.
For any rational number a, a ÷ 0 is not defined.
So rational numbers are not closed under division. two rational numbers can be added in any order. We say that addition is commutative for rational numbers. That is, for any two rational numbers a and b, a + b = b + a.
Multiplication is commutative for rational numbers. In general, a x b = b x a for any two rational numbers a and b.
If expressions on both sides are not equal. So division is not commutative for rational numbers.
Addition is associative for rational numbers. That is, for any three rational numbers a, b and c, a + (b + c) = (a + b) + c.
Subtraction is not associative for rational numbers.
Multiplication is associative for rational numbers. That is for any three rational numbers a, b and c, a x (b x c) = (a x b) x c.
Division is not associative for rational numbers
We say that 1 is the multiplicative identity for rational numbers.
a x 1 = 1 x a = a
We say that a rational number c/d is called the reciprocal or multiplicative inverse of another non-zero rational number a/b if 1 a/c= b/d =1.
Distributivity of Multiplication over Addition and Subtraction.
For all rational numbers a, b and c, a (b + c) = ab + ac
a (b − c) = ab − ac
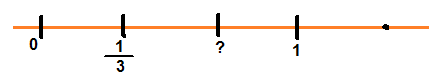
Any rational number can be represented on the number line in this way. In a rational number, the numeral below the bar, i.e., the denominator, tells the number of equal parts into which the first unit has been divided.
Finding a definite number of natural numbers (integers) between two natural numbers (integers).
you get countless rational numbers between any two given rational numbers.
Rational numbers are there between 1/10 and 3/10.
0/10, 1/10, 2/10 are rational numbers between the given numbers.
Another method finding the number between any two given numbers, we need not necessarily get an integer but there will always lie a rational number.
If a and b are two rational numbers, then a + b/2 is a rational number between a and b such that a < a + b/2 < b.
There you can find countless number of rational numbers between any two given rational numbers.
