The Mensuration is the branch of mathematics, in which we deals with the study of different geometrical shapes and their areas and Volume.
As we have learnt in the previous classes about the different shapes of area, perimeters etc.
Here we will also learn about surface area and volume of solids such as cube, cuboid and cylinder.
As the term recall means re-call means something call again or repeat something again.
Like we had use of area of square, perimeter of square and rectangle and many more.
|
Diagrams |
Shape |
Area |
|
|
Square |
b x h |
|
|
Rectangle |
a x a |
|
|
Triangle |
pb2 |
|
|
Circle |
a x b |
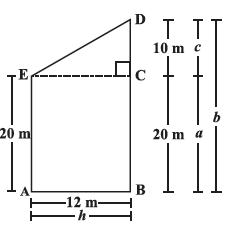
area of ABDE = 1/2h x C + h x a
= h (c/2a)
= h ( c + 2a/2)
= Height (Sum of parallel sides/2)
A general quadrilateral can be split into two triangles by drawing one of its diagonals.
This “triangulation” helps us to find a formula for any general quadrilateral
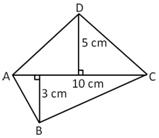
= (area of △ ABC) + (area of △ ADC)
= (1/2 AC x h1) + (1/2 AC x h2)
=1/2 AC x ( h1 + h2)
=1/2 d (h1 + h2) where d denotes the length of diagonal AC.
We split a quadrilateral into triangles and find its area. Similar methods can be used to find the area of a polygon.
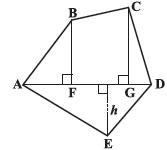
By constructing two diagonals AC and AD the pentagon ABCDE is divided into three parts.
So, area ABCDE = area of △ ABC + area of △ ACD + area of △ AED.
In your earlier classes you have studied that two dimensional figures can be identified as the faces of three dimensional shapes.
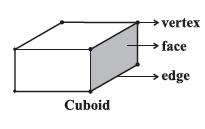
There are many way to find the total surface area, one of them finding the area of each face and then add. The surface area of a solid is the sum of the areas of its faces.
Total surface area of cuboid = 2 (h x l + b x h + b x l) = 2(lb + bh + hl )
Where h, l and b are the height, length and width of the cuboid respectively.
Cylinders are right circular shapes of cylinders.
The lateral (or curved) surface area of a cylinder is 2prh.
The total surface area of a cylinder = pr2 + 2prh + pr2
= 2pr2 + 2prh
= 2pr (r + h)
When any amount of space occupied by a three dimensional object is called its volume.
Volume of cuboid = area of the base x height
Volume of cube = l x l x l = l3
Volume of cylinder = area of base x height
= pr2 x h
= pr2h
There is not much difference between these two words.
Volume refers to the amount of space occupied by an object.
Capacity refers to the quantity that a container holds.
If a water tin holds 100 cm3 of water then the capacity of the water tin is 100 cm3. Capacity is also measured in terms of litres. The relation between litre and cm3 is, 1 mL = 1 cm3,1 L = 1000 cm3. Thus, 1 m3 = 1000000 cm3 = 1000 L.
