A triangle is a simple closed curve made of three line segments. It has three vertices, three sides and three angles.
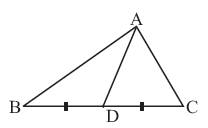
The line segment AD, joining the mid-point of BC to its opposite vertex A is called a median of the triangle.
As we learn about the triangle, a triangle is formed with three liens. Let's make a triangular shaped cardboard △ABC. Place it upright on a table. How ‘tall’ is the triangle? The height is the distance from vertex A.
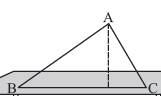
The height is given by the line segment that starts from A, comes straight down to BC , and is perpendicular to BC.
An altitude has one end point at a vertex of the triangle and the other on the line containing the opposite side. Through each vertex, an altitude can be drawn.
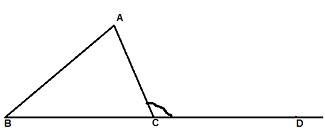
∠BCA is an adjacent angle to ∠ACD. The remaining two angles of the triangle namely ∠A and ∠B are called the two interior opposite angles or the two remote interior angles of ∠ACD.
In figure the ∠ABC formed at vertex C an exterior angle.
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
The total measure of the three angles of a triangle is 180°.
There is a remarkable property connecting the three angles of a triangle
By angle sum property of a triangle, ∠1 + ∠2 + ∠3 = 180°
A triangle in which all the three sides are of equal lengths is called an equilateral triangle.
A triangle in which two sides are of equal lengths is called an isosceles triangle.
The sum of the lengths of any two sides of a triangle is greater than the third side.
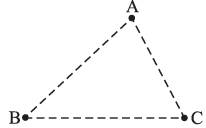
AB + BC ∠ AC
BC + CA ∠ AB
CA + AB ∠ BC
In a right-angled triangle, the sides have some special names. The side opposite to the right angle is called the hypotenuse; the other two sides are known as the legs of the right-angled triangle.

In △ ABC, the right-angle is at B. So, AC is the hypotenuse. AB and BC are the legs of ◺ABC.
There are four triangles in one square and the remaining four triangles in the other square.
Area of inner square of square A = The total area of two uncovered squares in square B.
a2 = b2 + c2
In Pythagoras property/theory
In a right-angled triangle, the square on the hypotenuse = sum of the squares on the legs.
Pythagoras says that for any right-angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the legs.
Pythagoras, a Greek philosopher of sixth century B.C. is said to have found a very important and useful property of right-angled triangles given in this section. The property is, hence, named after him. In fact, this property was known to people of many other countries too. The Indian mathematician Baudhayan has also given an equivalent form of this property. We now try to explain the Pythagoras property.
In a right-angled triangle, the sides have some special names. The side opposite to the right angle is called the hypotenuse; the other two sides are known as the legs of the right-angled triangle.
In a right-angled triangle, the square on the hypotenuse = sum of the squares on the legs.
