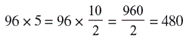Whole Numbers the natural numbers along with zero form the collection is known as whole numbers.
For Example-: 0, 20, 42, 100 etc. not 4.2, 1 / 2 etc.
Whole Numbers the natural numbers along with zero form the collection is known as whole numbers.
For Example-: 0, 20, 42, 100 etc. not 4.2, 1 / 4 etc.
The natural numbers along with zero form the collection of whole numbers.
Predecessor and successor
We have seen that the number 1 has no predecessor in natural numbers. To the collection of natural numbers we add zero as the predecessor for 1.
In given any natural number, you can add 1 to that number and get the next number i.e. you get its successor.
The successor of 16 is 16 + 1 = 17, 19 is 19 +1 = 20 and so on.
The number 16 has comes before 17, we can say that the predecessor of 17 is 17−1=16, 20 is 20 − 1 = 19 and so on.
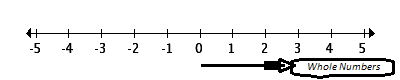
In the number line any number on the right from the Zero 0 will be Whole Number and after 0 is natural number.
Addition on the number line
Addition of whole numbers can be shown on the number line. By jumping like frog, from one number to another. Here you can see the Addition of 2 and 4.
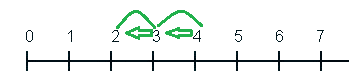

Start counting from 2 since we add 4 to this number so we can make 4 jumps to the right; from 2 to 3, 3 to 4, 4 to 5, and 5 to 6, so the result will be 6.
The sum of 2 and 4 is 6, i.e. 2 + 4 = 6.
Subtraction on the number line
The subtraction of two whole numbers can also be shown on the number line.
Here we can find 4−2.
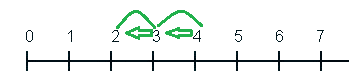
Here we start from 4. Since 2 is being subtracted, so move backwards left with 1 jump of 1 unit. Make 2 such jumps. We reach the point 2. We get 4−2 = 2.
Multiplication on the number line
Now we see the multiplication of whole numbers on the number line.
Let us find 2 x 5.
Start from 0, move 5 units at a time to the right, make such 5 moves. Where do we reach? we will reach at 10.
So, we say, 2 x 5 = 10.

After done various operations on numbers closely, we notice several properties of whole numbers.
Closure property : Whole numbers are closed under addition and also under multiplication.
Division by zero
Division by a number means subtracting that number repeatedly. So we can say Division of a whole number by 0 is not defined.
Commutative-: addition and multiplication are commutative for whole numbers.
After done various operations and properties on numbers line and with numbers closely, we notice several properties and patterns of whole numbers.
We can add with different way of whole numbers
107 + 9 = 116
107 + (10−1) = 116
We can Subtract with different way of whole numbers
107 - 7 = 100
107−(10-3) = 100
We can Multiplication with different way of whole numbers
84 x 9 = 84 x (10−1)= 756
We can Division with different way of whole numbers