As you have learnt about the number line and how to represent various types of numbers like — natural number, integers, fraction, decimal and so many.
Number system includes all the number types like - natural number, integers, fraction, decimal and so many.
If you looking the number line and continue in right direction from 0 you will have the collection of whole numbers which is denoted by the symbol W.
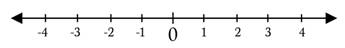
If you looking the number line and continue in left and right both direction from 0 you will have the collection of all integers, and it is denoted by the symbol Z. that has negative and positive both numbers collections.
To do this and make collection of so many numbers also like – rational numbers. The collection of rational numbers is denoted by Q. ‘Rational’ comes from the word ‘ratio’, and Q comes from the word ‘quotient’.
A number ‘r’ is called a rational number, if it can be written in the form p/q, where p and q are integers and q ≠ 0. (Why do we insist that q ≠ 0?)
There are infinitely many rational numbers between any two given rational numbers. That has learnt in previous class.
When a number cannot be written in the form p/q, than that number is called irrational where p and q are integers and q ≠ 0.
The numbers are called irrational numbers (irrationals), because they cannot be written in the form of a ratio of integers. There are many myths surrounding the discovery of irrational numbers by the Pythagorean, Hippacus of Croton.
Pythagoras, were the first to discover the numbers which were not rationals, around 400 BC. These numbers are called irrational numbers (irrationals), because they cannot be written in the form of a ratio of integers.
Hippacus has an unfortunate end, either for discovering that √2 is irrational.
Every real number is represented by a unique point on the number line. Also, every point on the number line represents a unique real number.
In the 1870s two German mathematicians, Cantor and Dedekind, showed that :
Corresponding to every real number, there is a point on the real number line, and corresponding to every point on the number line, there exists a unique real number.
This is why we call the number line, the real number line.
A number ‘s’ is called irrational, if it cannot be written in the form p/q, where p and q are integers and q ≠ 0.
A real number is either rational or irrational. So, we can say that every real number is represented by a unique point on the number line. Also, every point on the number line represents a unique real number.
This is why we call the number line, the real number line.
In the 1870s two German mathematicians, Cantor and Dedekind, showed that : Corresponding to every real number, there is a point on the real number line, and corresponding to every point on the number line, there exists a unique real number.
See how we can locate some of the irrational numbers on the number line.
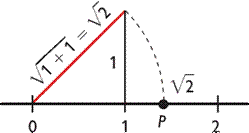
Here we will explain how to visualize and representation of real numbers on the number line using their decimal expansions.
It is true for all rationals of the form p/q (q ≠ 0). On division of p by q, two main things happen — either the remainder becomes zero or never becomes zero and we get a repeating string of remainders.
7/8 = 0.875.
When the decimal expansion terminates or ends after a finite number of steps. We call the decimal expansion of such numbers terminating means number that reoccurring such a respective.
Also 3.57272... can be written as 3572. So, all these examples give us non–terminating recurring (repeating) decimal expansions.
The decimal expansion of a rational number is either terminating or non-terminating recurring. Moreover, a number whose decimal expansion is terminating or non-terminating recurring is rational.
The decimal expansion of an irrational number is non-terminating non-recurring. Moreover, a number whose decimal expansion is non-terminating non-recurring is irrational.
As we had represent many numbers on the number line. Here we want to locate 2.665 on the number line. We know that this lies between 2 and 3.
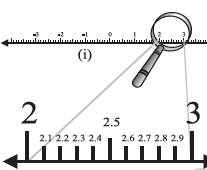
Every real number is represented by a unique point on the number line. Further, every point on the number line represents one and only one real number.
We learnt that the rational numbers satisfy the commutative, associative and distributive laws for addition and multiplication. Moreover, if we add, subtract, multiply or divide (except by zero) two rational numbers, we still get a rational number (that is, rational numbers are ‘closed’ with respect to addition, subtraction, multiplication and division). It turns out that irrational numbers also satisfy the commutative, associative and distributive laws for addition and multiplication. However, the sum, difference, quotients and products of irrational numbers are not always irrational.
We had lean in previous class about the exponent number that gives the factor of the number
Here we learn how to find the exponents of the real numbers.
So, for example:
172.17-5 = 17-3 = 1/173
