Linear Equations in two Variables

4.1 Introduction

We have studied linear equations in one variable. Here we learn more knowledge of linear equations in one variable shall be recalled and extended to that of two variables

4.2 Linear Equations

Consider the following equation: 2x + 5 = 0 in number line.

⇒ 2x+5 = 0

⇒ 2x = -5

⇒ X = -5/2

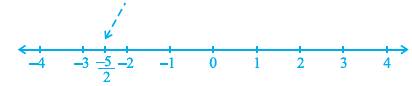
When any equation which can be put in the form ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables.

Here the equation ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables.

4.3 Solution of a Linear Equation

We have seen previously every linear equation in one variable has a unique solution.

A linear equation in two variables has infinitely many solutions.

4.4 Graph of a Linear Equation in Two Variables

We are learnt to obtained the solutions of a linear equation in two variables algebraically.

Here we will see at their geometric representation.

The solutions of the linear equation in Example 3, namely,  

x + 2y = 6

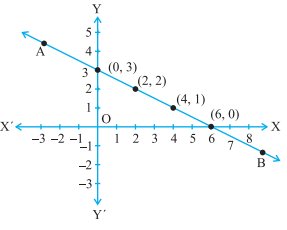
A linear equation in two variables is represented geometrically by a line whose points make up the collection of solutions of the equation. This is called the graph of the linear equation.

4.5 Equations of Lines Parallel to the x-axis and y-axis

The coordinates of a given point in the Cartesian plane.

In the the x-axis, the y-coordinate of each point is 0. In fact, every point on the x-axis is of the form (x, 0).